Summary: price spread for CSI300 and CSI500 spot/current month contracts show room for arbitrage. No spread for next month/current month contracts show room for arbitrage.
------------------------------------------------------------------------------------------------------------------------------
Graph 1: Future (Current Month)-Spot Arbitrage Opportunity for CSI300 contract (in the view of price difference)


Graph 2: Future (Current Month)-Spot Arbitrage Opportunity for SSE50 contract (in the view of price difference)

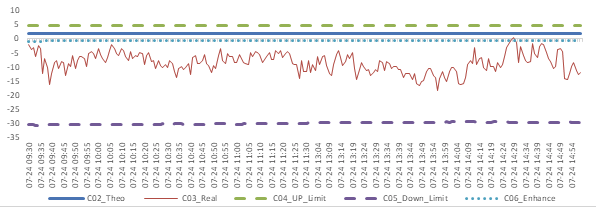
Graph 3: Future (Current Month)-Spot Arbitrage Opportunity for CSI500 contract (in the view of price difference)

Graph 4: Future (Next Month-Current Month) Arbitrage Opportunity for CSI300 contract (in the view of price difference)


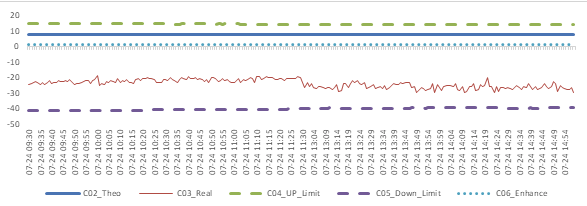
Graph 5: Future (Next Month-Current Month) Arbitrage Opportunity for SSE50 contract (in the view of price difference)

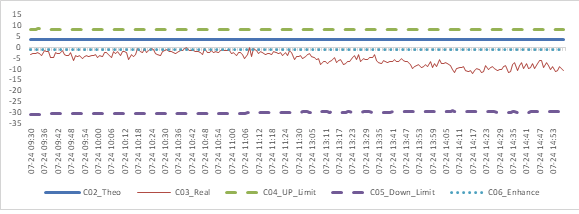
Graph 6: Future (Next Month-Current Month) Arbitrage Opportunity for CSI500 contract (in the view of price difference)


------------------------------------------------------------------------------------------------------------------------------
Assumption: risk-free rate (Rf): 3%; security borrowing cost (Rl): 8%; trading expense for spot (TCs): 0.025%; trading expense for futures (TCf): 0.005%; margin rates for futures contracts (Mf): 0.11 for CSI300 and SSE50, 0.13 for CSI500; margin rate for security borrowing (Ms): 0.3 (or 130% maintain rate).

When real price spread is out of theoretical range (calculated by our assumption), there exists absolute future-spot arbitrage opportunity. When real price spread is below the enhance line, there exists index enhancing opportunity.

For Future - Spot Arbitrage Opportunity:
Let St to be spot price, Ft to be current month future price, D to be dividend points. T to be current month future expiration date, t to be current time.
The theoretical price spread Theo=StExp(Rf(T-t))-PV(D)-St，the real price spread Real=Ft-St. With the tables and measures we mentioned:
（a）the up limit of non-arbitrage range is UP_Limit = Theo+(MfFt(EXP(Rf(T-t))-1))+(TCsSt+TCfFt)(EXP(Rf(T-t))+1)；
（b）the down limit of non-arbitrage range is DOWN_Limit = Theo-((1+Ms)St+MfFt)(EXP(Rf(T-t))-1)-(TCsSt+TCfFt)(EXP(Rf(T-t))+1)-St(Exp(Rl(T-t))-1)；
（c）the limit for enhance opportunity is Enhance = Theo -(MfFt(EXP(Rf(T-t))-1)-(TCsSt+TCfFt)(EXP(Rf(T-t))+1)；

For Next-month Future - Current-month Future Arbitrage Opportunity:
Let Fa to be current month future price, Fb to be next month future price, D to be dividend points. T0 to be current month future expiration date, T1 to be next month future expiration date, t to be current time.
The theoretical price spread Theo= Fa(t)Exp(Rf(T1-T0))-PV(D)-Fa(t), the real price spread Real = Fb(t)-Fa(t). With the tables and measures we mentioned:
(a) the up limit of non-arbitrage range is UP_Limit= Theo +[MfFb(t)(Exp(Rf(T1-t))-1)+MfFa(t)(Exp(Rf(T1-t))-Exp(Rf(T1-T0)))]-[TCf(Fa(t)+Fb(t))Exp(Rf(T1-t))+Fa(t)(TCf+TCs)Exp(Rf(T1-T0))+Fb(t)(TCs+TCf)]；
(b) the down limit of non-arbitrage range is DOWN_Limit = Theo -[MfFb(t)(Exp(Rf(T1-t))-1)+MfFa(t)(Exp(Rf(T1-t))-Exp(Rf(T1-T0)))+(1+Ms)Fa(t)(Exp(Rf(T1-T0))-1)]-[TCf(Fa(t)+Fb(t))Exp(Rf(T1-t))+ Fa(t)(TCf+TCs)Exp(Rf(T1-T0))+Fb(t)(TCs+TCf)]- Fa(t)(Exp(Rl(T1-T0))-1)；
(c) the limit for enhance opportunity is Enhance = Theo -[MfFb(t)(Exp(Rf(T1-t))-1)+MfFa(t)(Exp(Rf(T1-t))-Exp(Rf(T1-T0)))]-[TCf(Fa(t)+Fb(t))Exp(Rf(T1-t)) +Fa(t)(TCf+TCs)Exp(Rf(T1-T0))+Fb(t)*(TCs+TCf)]；